Toonladders
Toonladders zijn een opeenvolging van noten volgens een strak schema.
Er zijn talloze toonladders maar voor het doel van deze opleiding beperken we ons tot de Grote en Kleine toonladders.
Grote toonladders (Majeur)
Kenmerken:
- Klinkt vrolijk
- Tussen alle noten zit een hele toon behalve tussen de derde en de vierde en tussen de zevende en de achtste noot, waar slechts een halve toon tussen zit.
Het schema ziet er dus als volgt uit:
1 – 1 – ½ – 1 – 1 – 1 – ½
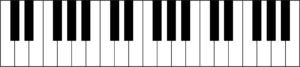
Als we de toonladder van DO-Groot bekijken op een piano klavier (enkel de witte toetsen) zien we dit duidelijk…
tussen de “MI en FA” en de “SI en DO” zit namelijk geen zwarte toets.
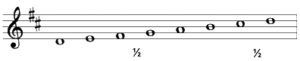
Als we bijvoorbeeld de toonladder van RE-Groot of MI♭-Groot willen bepalen dan moeten kruisen of mollen toevoegen tot het schema weer klopt.
RE-Groot:
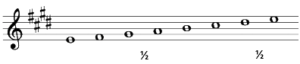
MI-Groot:
Toonladders met kruisen
Als we alle mogelijke toonladders met kruisen zouden bereken en sorteren deze vervolgens op het aantal kruisen, dan zien we dat het aantal kruisen van de volgende toonladder dezelfde kruisen heeft als de vorige +1 extra, … Dus de volgorde van de kruisen ligt vast!
SOL-Groot

RE-Groot

LA-Groot

MI-Groot

SI-Groot

FA♯-Groot

DO♯-Groot

Volgorde van de kruisen:
FA – DO – SOL – RE – LA – MI – SI
Nu kunnen we snel de voortekening bepalen van een toonladder met kruisen:
Want we weten:
- dat de laatste toonafstand in een grote toonladder ½ toon moet bedragen
- de volgorde van de kruisen
Voorbeeld 1:
Stel we willen de voortekening van RE-Groot bepalen:
Dan nemen we een ½ toon lager dan RE, dat is DO♯, en we gaan het rijtje van de kruisen af tot we aan DO(♯) komen, ofwel FA – DO.
De voortekening van RE-Groot heeft dus 2 kruisen
RE-Groot

Voorbeeld 2:
Stel we willen de voortekening van MI-Groot bepalen:
Dan nemen we een ½ toon lager dan MI, dat is RE♯, en we gaan het rijtje van de kruisen af tot we aan RE(♯) komen, ofwel FA – DO – SOL – RE.
De voortekening van MI-Groot heeft dus 4 kruisen
MI-Groot

Toonladders met mollen
Als we dezelfde oefening zouden maken voor alle toonladders met mollen zien we een soortgelijk patroon terugkomen. We merken tevens dat alle toonladders met mollen een ♭ in hun naam hebben, met slechts 1 uitzondering nl. FA-Groot (met 1 ♭). Dat is de enige toonladder waarvan je de voortekening moet onthouden.
FA-Groot

SI♭-Groot

MI♭-Groot

LA♭-Groot

RE♭-Groot

SOL♭-Groot

DO♭-Groot

Volgorde van de mollen:
SI – MI – LA – RE – SOL – DO – FA
Opvallend is dat de volgorde van de mollen het omgekeerde is van de kruisen!
Als we aandachtig kijken dan zien we dat het aantal mollen van de toonladder 1 méér is dan de positie in de volgorde van de mollen:
Voorbeeld 1:
Stel we willen de voortekening van MI♭-Groot bepalen:
Dan gaan we het rijtje van de mollen af en gaan ééntje verder dan MI♭, ofwel SI – MI – LA.
De voortekening van MI♭-Groot heeft dus 3 mollen
MI♭-Groot

Voorbeeld 2:
Stel we willen de voortekening van RE♭-Groot bepalen:
Dan gaan we het rijtje van de mollen af en gaan ééntje verder dan RE♭, ofwel SI – MI – LA – RE – SOL.
De voortekening van RE♭-Groot heeft dus 5 mollen
RE♭-Groot

Cirkel der Kwinten (Circle of Fifths)
Als we de toonafstanden tussen de kruisen bekijken in stijgende lijn dan merken we dat er telkens 3 ½ tonen tussen zitten. Deze toonafstand noemen we een kwint.
Als we de toonafstanden tussen de mollen bekijken in dalende lijn dan merken we ook hier telkens een kwint tussen zit:

Ter volledigheid een overzichtstabel met alle toonafstanden en hun naam:
| Prime | 0 tonen | |
| Prime | 0 tonen | |
| Secunde | 1 tonen | |
| Terts | 2 tonen | |
| Kwart | 2 ½ tonen | |
| Kwint | 3 ½ tonen | Fifth |
| Sext | 4 ½ tonen | |
| Septiem | 5 ½ tonen | |
| Octaaf | 6 tonen |
Kleine toonladders (Mineur)
Kenmerken:
- Klinkt droevig
- Tussen alle noten zit een hele toon behalve tussen de tweede en de derde en tussen de vijfde en de zesde noot, waar slechts een halve toon tussen zit.
Het schema ziet er dus als volgt uit:
1 – ½ – 1 – 1 – ½ – 1 – 1
Gelukkig moeten we de oefening van de grote toonladders niet herhalen, …
Er is een truckje!
Stel je wil de bijhorende kleine toonladder vinden van DO-Groot, dan tel je van DO anderhalve toon naar beneden.
Dus: SI – SI♭/LA♯ – LA.
la-klein is dus de bijhorende kleine toonladder van DO-Groot en heeft dus dezelfde voortekening als DO-Groot, d.w.z. geen kruisen of mollen.
la-klein

Andersom als je de voortekening wil zoeken van re-klein, dan tel van RE anderhalve toon naar boven.
Dus: RE♯/MI♭ – MI – FA.
FA-Groot is dus de bijhorende grote toonladder van re-klein en heeft dezelfde voortekening als FA-Groot, d.w.z 1 mol (of SI♭)
re-klein

Voorbeeld 1:
Stel we willen de voortekening van do-klein bepalen:
Dan gaan we anderhalve toon omhoog, ofwel MI♭
We bepalen vervolgens de voortekening van MI♭-Groot met de eerder geleerde technieken, ofwel 3 mollen (SI, MI, LA)
De voortekening van do-klein heeft dus 3 mollen.
do-klein

Van de kleine toonladder bestaan er 3 verschillende vormen:
Antieke vorm
Deze vorm is de basisvorm die we net hebben uitgelegd.
Harmonische vorm
Bij de harmonische vorm wordt de zevende noot van de toonladder met een halve toon verhoogd. Zo ontstaat er een vergrootte secunde (1 ½ toon i.p.v. 1 toon) tussen de zesde en de zevende noot, waardoor deze door veel mensen als “Arabisch” klinkend wordt ervaren.
Voorbeeld 1: la-klein harmonisch

Melodische vorm
Bij de melodische vorm worden zowel de zesde als de zevende noot met een halve toon verhoogd, maar enkel in stijgende lijn. In dalende lijn gebruikt men dan de antieke vorm.
Hierdoor heeft de melodische vorm veel meer weg van een grote toonladder.
Voorbeeld 1: la-klein melodisch
